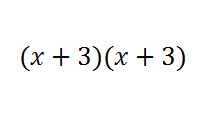The Use of Manipulatives Within the Classroom

Manipulatives are excellent tools that can be used within the classroom to help students understand abstract mathematical processes such as factoring. What are manipulatives though? Manipulatives are any type of object that a student can touch or move to help them learn a type of mathematical concept.

As mentioned earlier, one of the concepts that manipulatives can be used for is factoring. Factoring is a common mathematical process used to break down polynomials. When I was first introduced to factoring I was taught the many steps at how to factor a polynomial. For example, lets use:

To factor this equation a student would have to:

1) Find two numbers that multiply together to equal 9 but also add together to equal 6.

2) After figuring out that 3 and 3 both add together to 6 and multiply together to 9 the equation would have to be rewritten to:

3) The equation can then be broken apart where the student must know exponent rules and how the exponent rules work with variables as well:

4) Lastly the equation can be rewritten as a binomial:

After all of those steps this is the final outcome. For some students this can be easy if you follow the procedure and get your correct factors for step 1, but this is not simple for all students. As an alternative to the stepwise method of finding common factors, manipulatives can be used to acquire the same answer except visually. 

Some manipulatives that can be used to help with factoring are algebra tiles. In our class this week we used the 3 different sized algebra tiles to represent the variables and the two different coloured tiles to represent positive and negative.

 

Figure: Three different algebra tiles used as manipulatives to help with factoring equations.

Now lets try to factor that same equation using these algebra tiles as manipulatives. In order to do this properly the tiles need to be arranged within the box that they are stored in to help with the organization of terms.

 

Figure: Equation represented using algebra tiles.

The algebra tiles are arranged in a square (or sometimes rectangle) to represent the equation that is being factored. Now finding the factors for this equation is very simple once represented in this fashion! To find the factors you only use the "x" tiles and the "1" tiles along the borders of the box. 

Figure: Equation factored using algebra tiles.

The "x" tiles are placed adjacent to the xsquared tile and the number tiles are placed adjacent to the "x" tiles that are within the box. At the top border you have 1 "x" tile plus 3 "1" tiles representing x+3 and the same on the other border. These two equations are your factors for the overall equation!

A benefit to using manipulatives for topics such as factoring is that it allows students to apply the knowledge they learn in a fun way instead of being lectured by the teacher and just doing homework problems over and over again. I think this would be a much better way to help teach factoring to students!

"Perspective"

One of my fears as a future mathematics teacher is presenting my knowledge in a student friendly language that will help them best understand the content being taught. The reason why this is challenging is due to what I would call "mathematical perspective."

What is this "mathematical perspective" that I speak of? Well, in class this week we did an exercise that involved three rounds of a Tug of War between various creatures. The goal of the exercise was to figure out who would win the final Tug of War based on the outcome of the first two. 

Figure retrieved from: http://www.fotosearch.com/illustration/tug-war.html

The first Tug of War was a tie between 4 frogs and 5 fairy godmothers. The second Tug of War was also a tie between a 1 dragon on one side and 2 fairy god mothers and 1 frog on the other side. The final round had 1 dragon and 3 fairy godmothers on one side and 4 frogs on the other side, but the outcome was unknown. 

Like many mathematics problems, there is only one solution to this Tug of War but, there are multiple ways one could reach that solution (the dragon and fairy godmothers won). These multiple routes to the solution are based on your "mathematical perspective" or how you personally would solve a mathematical problem. 

, 

When our class of nine students was given this problem there were about three different methods to solve this problem, all giving the correct answer. In a high school classroom, this same outcome will likely occur where many different students will have various perspectives at solving mathematics problems. This activity showed us how many students even with the same academic background can look at mathematical problems from different perspectives.

As a future mathematics teacher, I would like to become more familiar with methods that allow me to cater to the various different mathematical perspectives that will be present within my classroom. One of the most interesting and frightening things to me when becoming a teacher is how every student learns differently, but I would like to do the best I can to help each student achieve their full potential.

Ryan

Introduction

My name is Ryan Alt and I am currently in my fifth year at Brock University in the I/S stream of Concurrent Education. My first teachable is chemistry and my second teachable is mathematics. 

I have always had an interest in mathematics and how mathematics can be used to describe so many different things in the universe. While growing up and going through the school system, mathematics was not always my strongest subject though. Along the way I hit a few road blocks, but those road blocks did not stop me from learning and enjoying mathematics. My goal as a future educator is to use my passion for mathematics to help students avoid the road blocks that I encountered and also help them gain a better understanding of the subject. 

Future posts on this blog will be reflections used to engage my learning and create new ideas with my colleagues at Brock University who are also aiming to become future mathematics teachers. This year I hope to learn how to effectively communicate my passion for mathematics through creative lessons and activities to give my students the best learning experience possible. 

This will be an exciting experience to share with everyone. I hope you enjoyed reading.

Ryan